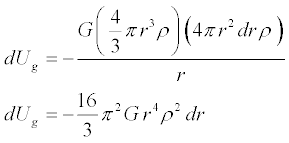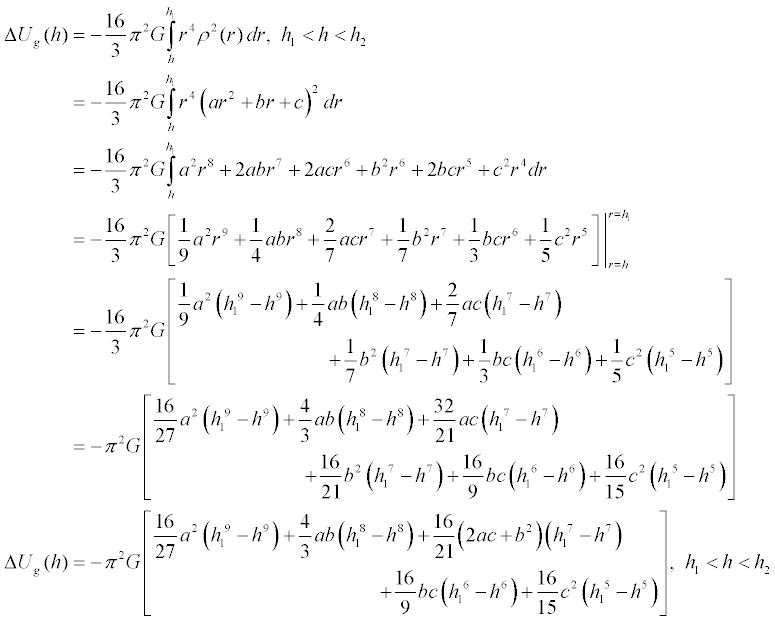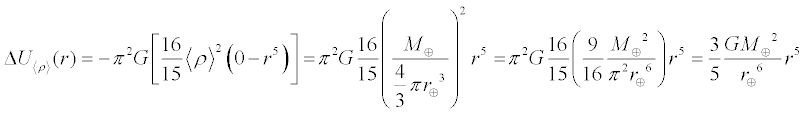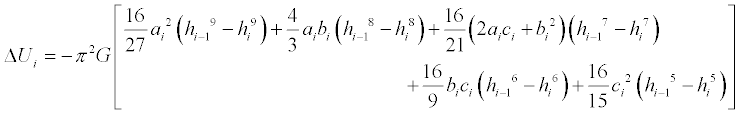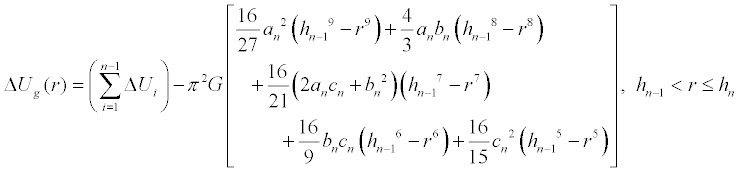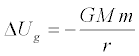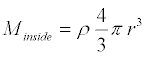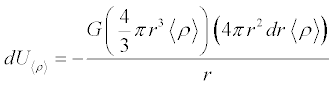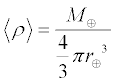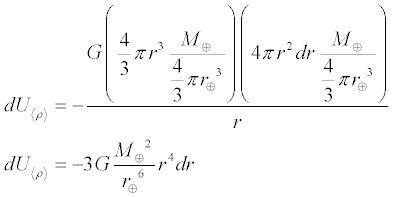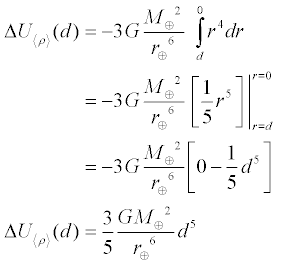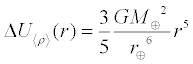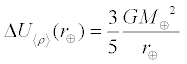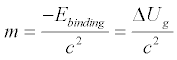So, how much energy would it take to disintegrate the Earth? Marvin the Martian wants to know!
Let's assume that to completely disintegrate something, we have to move all
of its pieces completely away from each other. In our case, we'll consider
only the gravitationally bound atoms and
molecules that constitute the Earth. The atoms within molecules are bound to
one another by the electromagnetic force. We want to stick solely to the
force of gravity for this analysis, so we'll not consider the ripping apart
of molecules.
By symmetry, the energy required to separate all the Earth's bits is equal
in magnitude but opposite in sign to the potential energy lost by the Earth's mass as it
assembled itself from the protoplanetary disk that once stood where the
solar system now exists. The gravitational binding energy (also called
gravitational self energy) of a system of particles is the change in the system's potential energy as all its bits fell to the
bottom of the system's gravitational potential well.
Or, we can approach it from the other direction: the binding energy is the
opposite of the system's change in potential energy as its bits are moved an infinite distance apart.
This works as well for gravitationally bound systems like planets as it does
for molecules bound by the electromagnetic force and atomic nuclei bound by
the strong nuclear force. In the case of the Earth, its gravitational
binding energy is equal in magnitude and opposite in sign to the energy required to move its gravitationally bound
atoms and molecules an infinite distance apart.
So how do we know how much energy it would take to move all
those bits apart? It's simply the change in potential energy as the bits are
separated. So how do we find the change in potential energy? Like
this.
Through the work-energy theorem, we know a system's change
in potential energy is the negative of the integral of force over a
distance. This is discussed in greater depth in the Gravitational Potential essay. For the force of gravity, we have
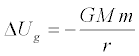
where
|
|
|
|
| ΔUg |
= |
Change in gravitational potential energy, J |
| G |
= |
6.6743×10-11 m3·kg-1·s-2 |
Universal gravitational constant 1 |
| M |
= |
Mass of one object, usually the larger,
kg |
| m |
= |
Mass of another object, usually the
smaller, kg |
| r |
= |
Distance between the objects' centers of
mass, m |
To apply this relationship to the problem of finding the
gravitational binding energy of the Earth, we imagine removing one
infinitesimally thick outer shell after the other from a spherical
distribution of mass that gets smaller and smaller as shells are removed.
Each mass shell is moved an infinite distance away through the diminishing
force of gravity between the shell and sphere. It will take some energy
to move all these shells; that energy is the negative of the binding energy of the system.
To find energy needed to remove all these shells, we will find the change in
the system's potential energy. To find the change in potential energy, we need to know the mass of the shell, the mass of the
remainder of the sphere, and the force through which we're moving the shell.
The mass of any volume is simply density times volume. Each shell has a
volume given by its area times its thickness and a mass given by its volume
times its density. In short, we have
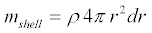
where ρ is the density of the shell, r is the radius of the shell, and dr is the thickness of the shell.
The remainder of the sphere inside the shell will
have a mass given by
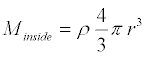
where ρ is the density of the sphere and r is the radius of the sphere.
If we assume that the density of the sphere is the same everywhere, then
each shell contributes an infinitesimal portion of potential energy as
described by
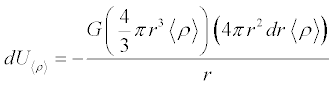
where the average density is given by
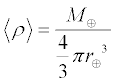
where the angle brackets indicate an average value and Å is the astronomical symbol for Earth. (It's actually the Boolean
exclusive-or operator, but close enough.)
Substituting, we obtain
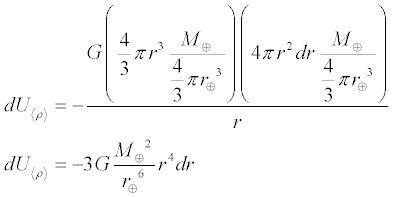
To find the total change in potential energy as all the shells are removed
by summing all the infinitesimal bits of potential energy, we integrate over the
radius of all the shells, from the outside to the inside, like this
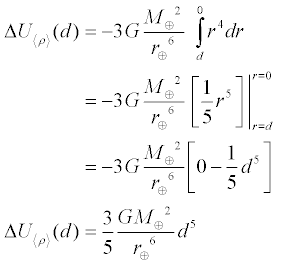
Thus for any point within the sphere, the change in potential energy using
average density is
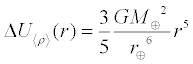
Therefore the total change in potential energy as the Earth is disassembled using average
density becomes
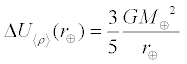
If, on the other hand, we do not wish to assume a constant
density throughout the Earth, we'll need a density that varies with radius.
We can approximate the Earth as a sphere having several layers, each layer
having a quadratic density function as described in the Earth Gravity essay. In short, we have a
piecewise density function.
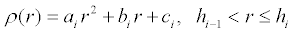
where r is the distance from the center of the Earth and where
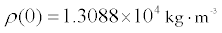
and where the indexed constants for each piece of the function are described
in the table below.
|
| i |
Layer |
Height hi (m) |
ai (kg·m-5) |
bi (kg·m-4) |
ci (kg·m-3) |
| 1 |
Inner core |
1.2215×106 |
-2.1773×10-10 |
1.9110×10-8 |
1.3088×104 |
| 2 |
Outer core |
3.4800×106 |
-2.4123×10-10 |
1.3976×10-4 |
1.2346×104 |
| 3 |
D'' layer |
3.6300×106 |
0 |
-5.0007×10-4 |
7.3067×103 |
| 4 |
Lower Mantle |
5.7010×106 |
-3.0922×10-11 |
-2.4441×10-4 |
6.7823×103 |
| 5 |
Inner transition zone 1 |
5.7710×106 |
0 |
-2.3286×10-4 |
5.3197×103 |
| 6 |
Inner transition zone 2 |
5.9710×106 |
0 |
-1.2603×10-3 |
1.1249×104 |
| 7 |
Outer transition zone |
6.1510×106 |
0 |
-5.9706×10-4 |
7.1083×103 |
| 8 |
Low velocity zone & lid |
6.3466×106 |
0 |
1.0869×10-4 |
2.6910×103 |
| 9 |
Inner crust |
6.3560×106 |
0 |
0 |
2.9000×103 |
| 10 |
Outer crust |
6.3680×106 |
0 |
0 |
2.6000×103 |
| 11 |
Ocean |
6.3710×106 |
0 |
0 |
1.0200×103 |
Going back to our expression for the mass of the shell and the mass of the
sphere inside the shell, we now have the following infinitesimal potential
energy, this time using the real density instead of an average density.
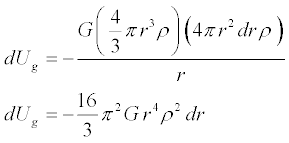
Same as before, to sum all the infinitesimal bits of binding energy we
integrate over the radius of all the shells from the outside in. This
time, however, we can only integrate one layer at a time since the piecewise
density function is not differentiable across the layer boundaries.
We'll first derive a relationship for all the infinitesimal shells within
one layer, then we'll sum the layers.
For a point having a radius
within a given layer, we will need to find the potential energy change that
occurs as that layer is stripped, shell by shell, from the radius of the
point in question to the inside of the layer. For a point h in a
layer having lower and upper bounds of h1 and h2 respectively, we have
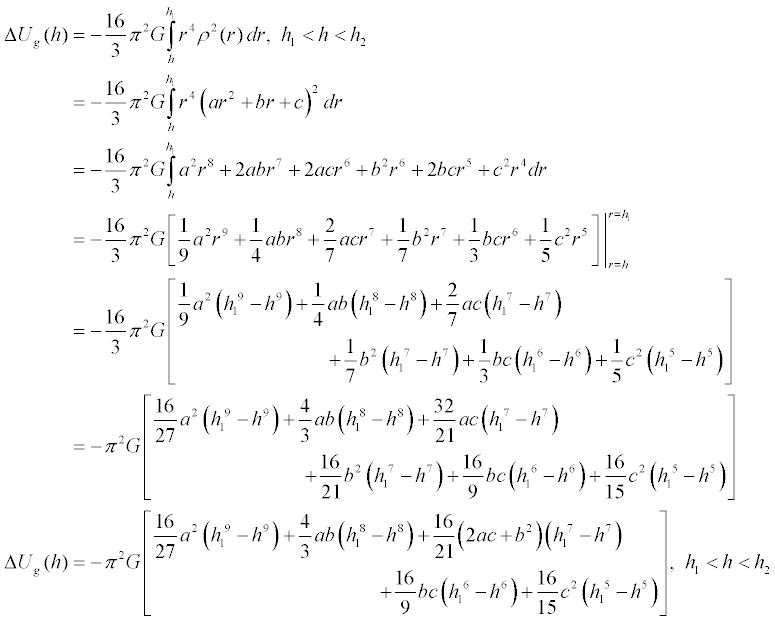
Which can be seen to reduce to the equation for average density by assuming
a sphere of one layer where a = b = h1 = 0
and c = <ρ>
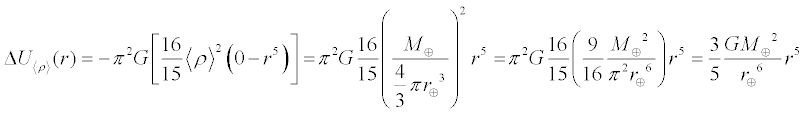
We can also see that for the entire ith layer we have
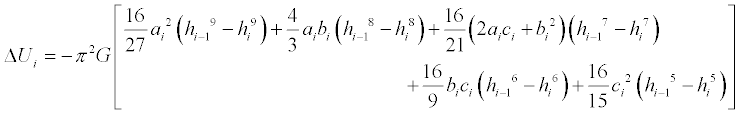
and thus for any point r along the radius of the sphere, we have
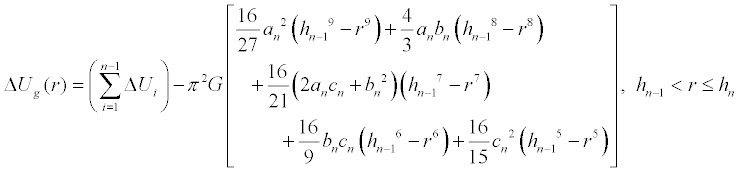
where ΔU0 = 0 and the indexed constants for each piece of the function are described in
the table above.
And since the gravitational binding energy is the same magnitude but
opposite in sign to the change in potential energy as the system is
disassembled, we have
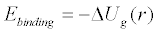
Using the average density of the Earth = 5.51394×103 kg·m-3 as calculated in the Earth Gravity essay along with the variable
density function discussed above, we obtain the following energies.
Average Density Method:
the Earth's gravitational binding energy is -2.242×1032 J
Variable Density Method:
the Earth's gravitational binding energy is -1.711×1032 J
Thus, while the average density method figure is in the
ballpark, it is too high by 31.05%.
Note that the binding energies listed above are negative. This is often a
source of unnecessary confusion.
Remember, we define the binding energy as the change in the potential
energy of the system as it gravitationally assembled itself. That means the binding energy
is also the negative of the change in potential energy as its pieces are
separated back to infinity. As the bits are separated, the change in
potential energy is positive: it takes an input of energy to separate two
masses that are held together by the force of gravity. Therefore, the change
in potential energy is negative as the system gravitationally collapses—and
therefore the binding energy is negative.
We can also look at this the other way around. If the system requires an
energy input to become separated, then the system must have an energy output
as it collapses. It does: in the case of a planet, this energy is
called the heat of accretion. All that gravitational potential energy of the
protoplanetary disk got converted to heat as all its bits condensed under
the force of gravity to form the Sun and the planets. Some of the original
gravitational potential energy is still around: the planets have not
collapsed into the Sun.
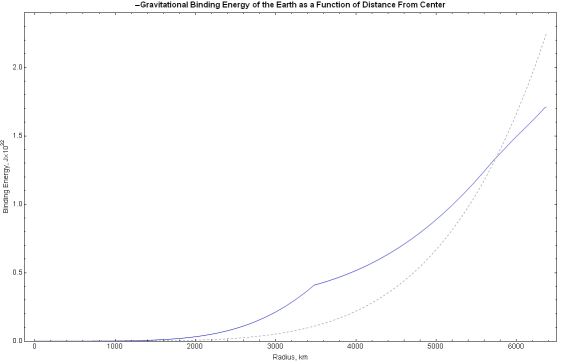
If we plot the average and variable density binding energy functions over the radius of the
Earth, we obtain the following; the blue line represents the variable
density function and the dashed line is the average density approximation.
Click on the plot thumbnail for a high resolution image best viewed with a
1280x1024 screen resolution. The
Mathematica source code may be found here.
One place in which gravitational binding energy becomes
important is in the Nordtvedt effect, which is a test of the equivalence
principle envisioned by Kenneth Nordtvedt. 4,5,6,10
The equivalence principle posits that inertial mass—mass
used by F = ma, Newton's second law—is identical to
gravitational mass—mass used by the law of universal gravitation. Nordtvedt showed that some theories of gravitation predict that
gravitational binding energy will affect gravitational mass, but not
inertial mass. 6,10
In short, a system of particles loses gravitational potential energy as it
undergoes gravitational collapse. As such, the collapsed state has a lower
total energy, the difference in energy being the gravitational binding
energy. Since the system has a lower total energy, it also has a lower
total mass by E = mc2. Or does it? The
existence of the Nordtvedt effect would mean that gravitational binding
energy reduces the gravitational mass of the system as it collapses,
while the inertial mass of the system remains constant. 4
As such, perhaps the Earth's gravitational mass is not equal to its inertial
mass by a small fraction. But how small a fraction?
We can convert the Earth's binding energies to mass via
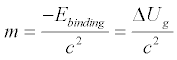
where c = the speed of light = 2.99792458×108 m·s-1. 2
Then, we can then find the binding energy mass fraction based on an Earth mass of
5.9736×1024 kg. 3
We end up with the following figures for the Earth.
| Method |
Binding Energy (J) |
Mass Equivalent (kg) |
Mass Fraction |
| Earth Average Density |
-2.242×1032 |
2.495×1015 |
4.177×10-10 |
| Earth Variable Density |
-1.711×1032 |
1.904×1015 |
3.187×10-10 |
Thus, the Earth's gravitational mass might be less that its inertial mass by
up to 320 parts per trillion. So, how might we go about detecting
this difference? When Nordtvedt discussed the effect, he came up with the
idea of using the Moon as a reference.
We can perform the same calculations for the Moon and obtain
| Method |
Binding Energy (J) |
Mass Equivalent (kg) |
Mass Fraction |
| Moon Average Density |
-1.245×1029 |
1.385×1012 |
1.885×10-11 |
| Moon Dual Density |
-1.223×1029 |
1.361×1012 |
1.852×10-11 |
where 3,7
|
|
|
|
| Lunar mass |
= |
7.349×1022 kg |
| Lunar volumetric radius |
= |
1.7371×106 m |
| Average lunar density |
= |
3.347×103 kg·m-3 |
| Lunar core radius |
= |
3.50×105 m |
| Lunar core constant density |
= |
7.2 kg·m-3 |
| Lunar mantle constant density |
= |
3.315×103 kg·m-3 |
In this case, the average density method figure is only 1.80% above the dual
density figure. This is expected; the core is dense but very small; and,
we're assuming a constant density in the core and the mantle. Having a better density profile
for the Moon would make the variable density function more accurate.
If we plot the average and variable density binding energy
functions over the radius of the Moon, we obtain the following; the blue
line represents the dual density function and the dashed line is the
average density approximation.
Click on the plot thumbnail for a high resolution image best viewed with a
1280x1024 screen resolution. The
Mathematica source code may be found here.
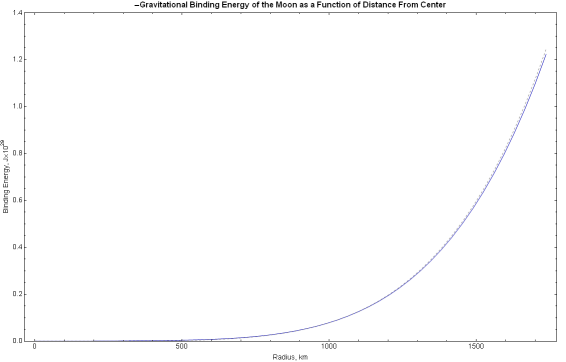
Even though the lunar density profile isn't very accurate,
it's accurate enough to show that the gravitational binding energy mass
fraction of the Moon—20 parts per trillion—is
over an order of magnitude smaller than that of the Earth. That being
the case, if the Nordtvedt effect exists, then the
Moon would react to the Sun's gravitational field to a greater degree than
the Earth. The Moon's ratio of gravitational mass to inertial mass would be
higher than the Earth's and the equivalence principle would be shown to have
a loophole. If the Nordtvedt effect operates at its theoretical maximum, the
Moon's orbit should be elongated along the Earth-Sun
radial by an amount on the order of ten meters. 4
Using the retroreflectors left on the lunar surface during the Apollo
missions, the Moon's distance can be determined with lasers to millimeter
accuracy. 8 To date, the Moon's orbit has not been observed to be measurably
polarized along the Earth-Sun radial to any degree at all. The Nordtvedt effect remains
unobserved. 8,9,10,11,12 Therefore, if the Nordtvedt effect exists
at all, it is quite small.
Notwithstanding possible violations of the
equivalence principle, Marvin has his work cut out for him.
The power output of the Sun is 3.846×1026 Watts.2
The complete gravitational disintegration of the Earth would require an
input of energy equivalent to the Sun's total output for a continuous 5
days, 3 hours and 34 minutes. Perhaps ten days with a hyperbolic
mirror of fractional AU aperture. Place the Sun at one focus and the Earth at
the other. It won't be cheap.
One megatonne TNT nuclear equivalent is 4.184×1015 Joules, so
you'd need about 1.4 million-billion 30 megatonne thermonuclear warheads to blow
up the planet.13 Not even in General Curtis LeMay's wildest
dreams would such an arsenal exist, although the Earth certainly contains
enough fissionable and fusible material.
Antimatter has the advantage of total annihilation with matter, converting
200% of its mass energy to pure energy in so doing. As such, one would
require 950
billion metric tons of antimatter to do the job. One will also need a large
containment vessel and a nearly infinite supply of patience as Fermilab's
current antiproton production capacity is about 1.5 nanograms per year. 14
References
1 NIST - CODATA Value: Newtonian constant of gravitation.
2 NIST - CODATA Value:
Speed of light in vacuum.
3 NASA/GSFC -
Planetary Fact Sheets.
4 Battat, James - Nordtfedt Effect Overview.
5 Wikipiedia - Equivalence Principle.
6 Will, Clifford - The Confrontation between General
Relativity and Experiment.
7 Khan, A., et al. - The Core of the Moon - Molten or
Solid?.
8 Apache Point Observatory Lunar Laser Ranging Operation.
9 Baeßler, S., et al. - Improved Test of the Equivalence
Principle for Gravitational Self-Energy.
10 Nordtvedt, K. - Lunar Laser Ranging - a comprehensive
probe of post-Newtonian gravity.
11 Williams, J., et al. - Progress in Lunar Laser Ranging
Tests of Relativistic Gravity.
12 Williams, J., et al. - Lunar Laser Ranging Tests of
the Equivalence Principle with the Earth and Moon.
13 Wikipiedia - TNT Equivalent.
14 Schmidt, G., et al. - Antimatter Production for
Near-term Propulsion Applications.
|